数字と文字の積で表されたもの、たとえば2x, xy, z²などを項とよぶ。数字だけの2、１０なども項である。次数とは掛け算されている文字の個数を表すもので、2xではｘが一個なので次数は１，xyは2つの文字が掛け算されているので次数は２，z²はｚが2個なのでこれも次数は2である。数字だけの項は文字が無いので次数0である。文字の前に掛かっている数字は係数と呼ばれる。

2xとかxyなどの項だけの式を単項式という。ここで、式というのは2xのように２とxの関係を数学記号を用いて表現したものである。ちなみに、2xというのは掛け算記号である×が省略されている。２＋３＝５というのも式である。つまり、2という数字に3を足す（+）とその結果（=）は5となるという関係を数学記号を使って表現したので、これも式である。2x+xyというのは項が2xとxyの2つを結び付けている式なのでこれを2項式という。したがって、2+3=5は3つの項を結び付けているので3項式となる。単項式以外を多項式という。多項式2x+xy+xyzの次数はxyzの３次が一番大きいのでこの式の次数は３である。

x²-8x+12というのは2次の3項式である。

ちなみに、項の次数がすべて同じ式のことを同次式または斉次式という。例えば、

x+y : 2変数の1次式
x²+xy+y² : 2変数の2次式
xy : 2変数の2次式

非同次式は項の次数が同じでない式のことをいう。例えば、

x²+2y : 2次の項と1次の項が混在している
x²+xy+y²+1 : 定数項が0次、その他が2次
x²-8x+12　: 2次の項、1次の項、0次の項が混在している

以上の式は変数が根号(ルート）に含まれない有理式である。もし根号の変数が含まれる項があるとき、例えば、

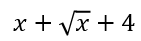
は無理式、また、次式のように分母に有理式がある場合は

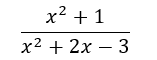
分数式という。

方程式とは何であろうか？

例えば、x-2=8と書かれているものは方程式であり、この関係を満足するｘを求めることが目的になっている。この関係を満たすｘは-2を右辺に移項して x=8+2=10と計算できる。このｘ＝１０を求めることを要求しているのが方程式である。

これに対して、2x+4x　は式であり、この演算の結果は？と求められたら、2x+8x=6x　と記述するのが式である。つまりこの場合、この関係を満たすｘを求めるわけではないので、単に式という。