同次連立一次方程式をもう一度見てみよう。
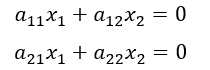
であり、これを行列を使って表すと、
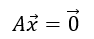
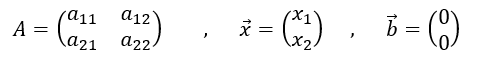
であった。いま係数行列の列を次に示すようにベクトルで表すと、
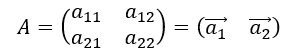
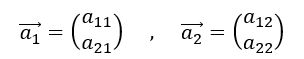
である。同次連立一次方程式はこれを使うと次のように書ける。
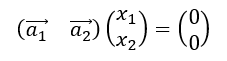
または、
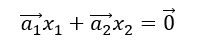
もし、x1 = x2 = 0 であれば、この式はどのようなベクトルを持ってこようが必ず成り立つ。この時x1, x2は自明解というのであった。この場合の二つのベクトルはそれぞれ一次独立の関係にあるという。これら2つのベクトルを図に示すと、
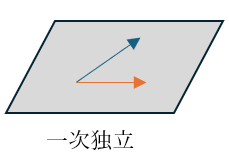
であって、一つの平面を形成する。言い換えれば2つの一次独立なベクトルは一つの平面内にあるともいえる。
さて、ベクトルを成分表示して、同次連立一次方程式をもう一度書き直してみよう。
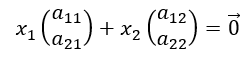
これを展開すると
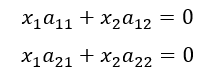
元の連立方程式に戻るわけであるが、これからx1, x2を求めると、
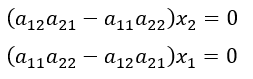
と表わされるが、もともとx1 = x2 = 0を仮定していたわけであるから、ベクトルがゼロベクトルでない限り、上式に共通するカッコ内の値はゼロではないことになる。すなわち、

これは
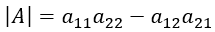
であるから、二つのベクトルの成分で作る行列Aの行列式がゼロでないとき、この二つのベクトルは互いに一次独立の関係にあるといえる。
これに対し、|A|=0 のときは、二つのベクトルは一次従属であるといい、これら二つのベクトルは重なっていて、これらを含む平面を決定することが出来ない。言い換えれば無数にあると言っても良い。図に表すと、