同次連立一次方程式の解を考えてみよう。同次連立一次方程式というのは連立一次方程式の定数項が全て０であるものをいう。すなわち、

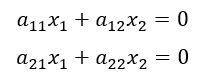
であり、行列を使って表すと、

ここに、

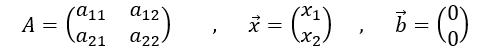
である。この方程式では

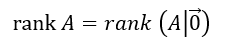
であるので、必ず解を持つ。ただし、どのような解であるかは次の条件で分類できる。

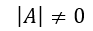
の場合、必ず逆行列　A^-1　を持ち、解はただ一つ、(0, 0) である。つまり2つの直線は原点で交わる。この解を自明な解という。ちなみにrank A =2 である。

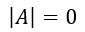
の場合、解は無数に存在する。この時rank A=1 < 2であるので、2つの直線は原点を通ってお互いに重なっているため、その直線状の点はすべて解となる。これらの解を非自明な解という。

例えばx₁₁を任意の定数をsと置くと、x₁₂は-(a₁₁/a₁₂)×sで表されるので、まとめると

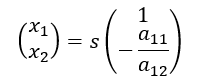
と求められる。