レイノルズ輸送理論式の B に流体の運動量 mu を選ぶと、流体の運動量の時間変化を調べることによって外力を見積もれることになる。流れの中にある物体から流体に力を与えて流体の運動量の変化をもたらすという事は、逆に言えば反作用として流体がその物体に力を与える。したがって検査体積の入口出口それぞれにおける運動量の時間変化の差 がすなわち流体が受けた力となるので、逆に流体がその物体に力を与えたことになる。

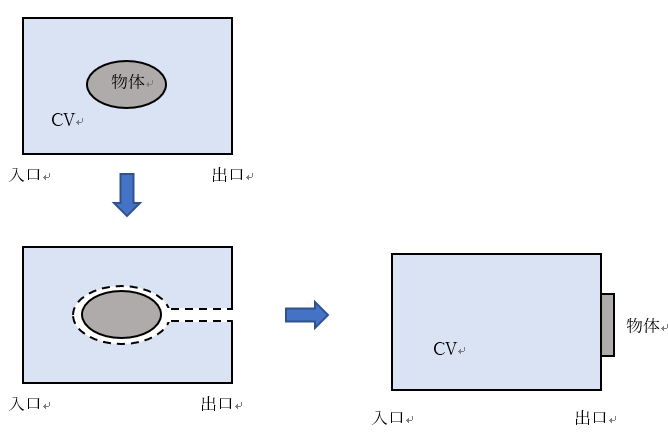
なお、CV中に物体を入れると物体によって流体に与える力は表面力となるので図の様に後ろから切れ目を入れて、物体をCVの外にあるものと考えるようにして、物体から与える力をCVの表面力としてみなせるように工夫する。したがって、力を見積もる際のCVは右下の図のイメージとなる。

今流体の運動量をB=M と書くと、レイノルズの輸送方程式から、

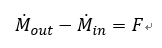
となり、Fが物体によって流体に与えた外力となり、その結果流体の運動量を変化させる。逆に流体が物体に与えた力はF_b=-F で与えらえる。

入口の断面積をA₁, 流入速度をu₁とし、出口の断面積をA₂, 流出速度をu₂とすると、

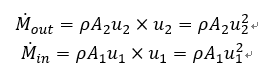
と書けるので、流体が物体に与える力は

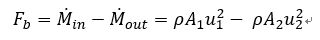
と書くことができる。