例えば、2つの一次方程式に共通するx1とx2を求めるというのが2つの方程式を解くということになる。

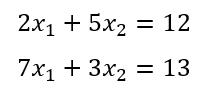
を変数の係数を合わせて消去していく方法で解いてみよう。このやり方は中学校の数学で習って以来行っているので慣れ親しんでいるであろう。

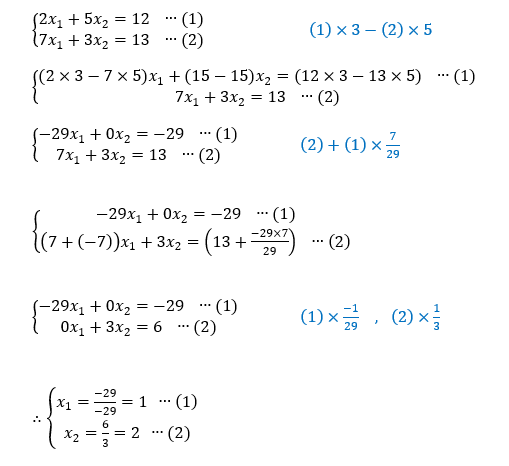
まず式に番号を付けて、（１）の式からx₂を青字で書いた操作によって消す、同様に（２）の式からx₁を消去するという手順である。最後はx₁とx₂の係数はそれぞれ1となるようにすれば、自然と解が求まるという仕組みである。

これを行列の行基本操作を使って解いてみよう。まず、連立方程式を行列を使って表現し、係数行列と定数行列を合わせて拡大係数行列を作る。

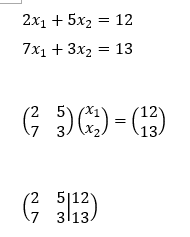
行列というのはこのように係数を変数（x₁,x₂）や等号（＝）を省いて、正方形、長方形に並べたものである。横方向の並びを行、縦方向の並びを列と称している。最後の表現を拡大係数行列と言って、変数の係数と定数を縦棒で区切って書いたものである。消去法と並べて対比して下に記す。

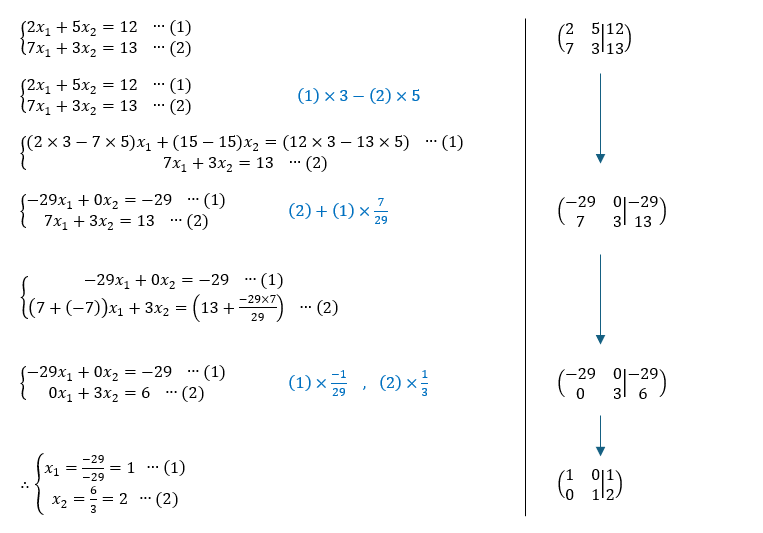
行が式に相当する。式に掛け算したり足したり引いたりして、対角線上に1を並べた形にもっていくことを行基本操作と呼んでいる。なんてことはない、消去法でやっていること同じことをやって、係数行列の対角線上の値を1にするのである。つまり行列で表した方程式が次のようになったことになる。

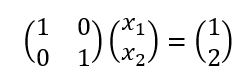
これが、

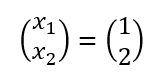
を表しているので、x₁=1、x₂=2と求まったことを意味している。