２つの未知数 x₁, x₂を持つ1次方程式の連立方程式の例を以下のように書く。

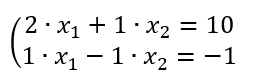
ここで未知数の前についている係数を並べて次のように行列で書いたものを係数行列という。

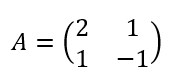
等式の右辺の定数を縦に並べたものを列ベクトル（１列の行列）という。ベクトルなので頭に矢印をつけてある。

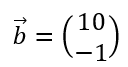
これらを一行にまとめた行列を拡大係数行列という。

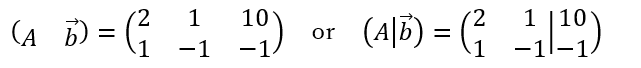
たての棒は係数と定数を区別するために付けてある。この方が混同しなくて済む。

なぜこんなことをするのかというと、ひとえに見やすく、扱いやすく（解きやすく）するためである。

ちなみに未知数を列ベクトル

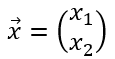
に書いて、連立方程式を書き直すと、次のように書ける。

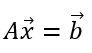
すなわち、

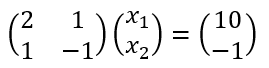
すっきりと表現できる。今この例では、2つの連立方程式だが、３つ、４つと増えても、このルールで拡張できる。例えば、未知数が3（n=3）で、3本の方程式だとすると、

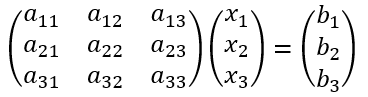
すなわち、これは以下の連立方程式である。

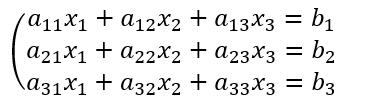
これを拡大係数行列を使って書き表すと、

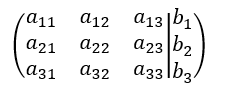
となる。