理想気体が状態1から状態2に変化した時のエントロピー変化を求めておこう。まず、可逆過程におけるエントロピーの定義と熱力学第一法則から、
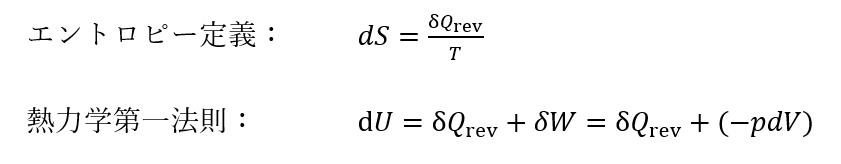
である。
これら二つの式からδQrev を消去すると、
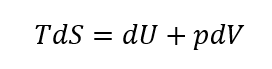
と書ける。これをギブスの式という。また、これをエンタルピーの定義、H=U+pVを使って書き換えてみよう。まず、このエンタルピーの両辺を微分すると、
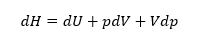
と書ける。これを用いて、ギブスの式から dU を消去すると、
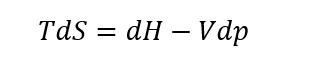
を得る。したがって、 dS の表現として2つの式を得る。すなわち、
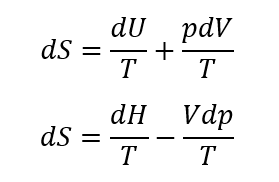
である。すなわち、これらの式には過程に依存する δQrev が含まれていないので、エントロピー変化を状態量の変化として他の状態量の変化で求めることができる。ここで、理想気体の状態方程式であるpV=nRT、内部エネルギーおよびエンタルピーの表現である dU=mcvdT、dH=mcpdT を用いて、エントロピー変化を表すと、
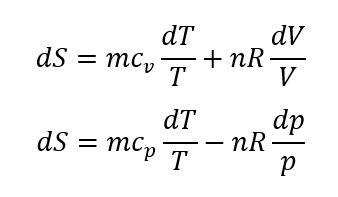
である。これらの関係を用いて、状態1から状態2に変化した時のエントロピー変化を、等温変化、等積変化、等圧変化のそれぞれで求める。
等温変化 dT=0 :
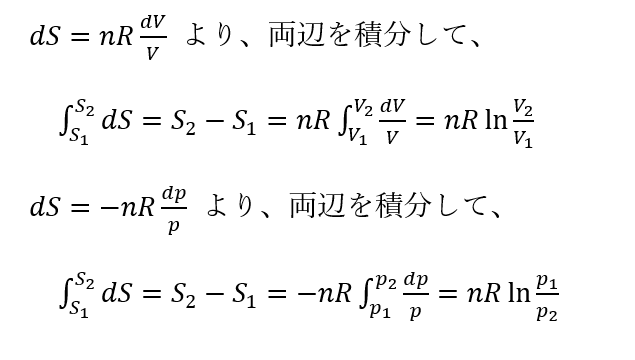
等積変化 dV=0:
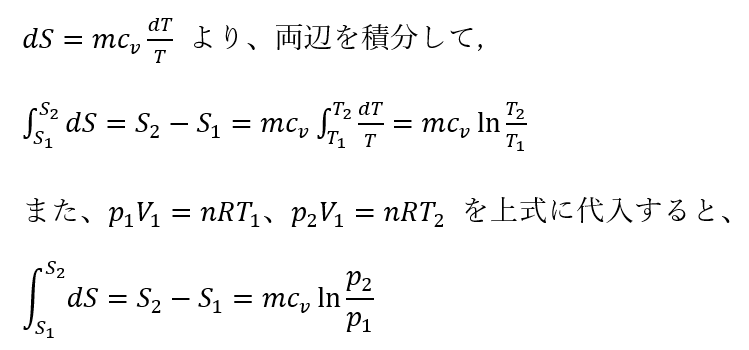
等圧変化 dp=0:
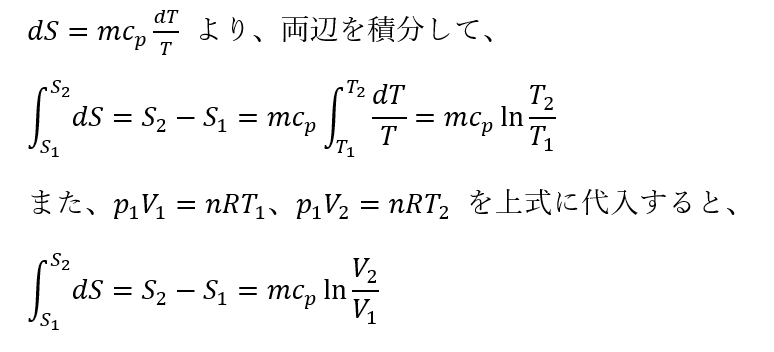
を得る。
断熱変化では δQrev=0 なので、エントロピー変化 ΔS=0 である。
















