仕事 W [J]というのは力 F [N] ×力の方向に移動した距離 x [m] で表されるものである。ジュールという単位 [J] は [Nm] という単位を一文字で書いたものである。つまり、仕事を成した結果は物体に力を加えてその方向に移動させることで目で見える形で示すことができる。このジュールという単位はエネルギーの単位と同じであるから、エネルギーを使って仕事を成すには力に変換しなければならない。物体(システム)の周囲(外界)から力(外力)が作用して物体が移動するので、仕事をしたのは外界であり、仕事がされたのは物体である。これを図に示すようなシリンダ内を動くピストンで構成されたエンジンで見てみよう。燃焼ガスが発生させる圧力 p {Pa] がピストンヘッドの断面積 A [m2] に作用する。ピストンヘッドの形状が直径 d の円であれば、面積 A=(d/2)2π である。この直径 d をボア径という。圧力は単位面積当たりの力なので、単位は[N/m2]であるがこれを [ Pa (パスカル) ]という一文字で書く。したがって、燃焼ガスが出す力 F は F=pA [N] である。この力(外力)によって物体であるピストンをシリンダ内壁に沿って x [m] だけ移動させる。この移動距離はエンジンではストロークと呼ばれる。
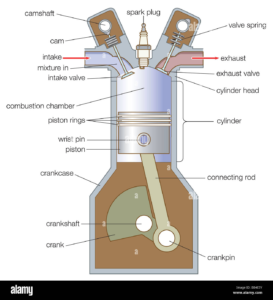
したがって、このエンジンで取り出せる仕事は、W=Fx=pAx=pV と表わせる。ここに V はAx であるので、シリンダのヘッド断面積 A×移動した距離xというのはシリンダが移動した体積となる。すなわち、燃焼ガスが膨張した体積でもある。すなわち、ピストンに力を与えた外界の燃焼ガスが膨張によって仕事をピストンに与えたと言える。その仕事の大きさは燃焼ガスの発生する圧力×体積膨張で表される。つまり、仕事を取り出すには気体の膨張を使うのである。
この燃焼ガスは気体の状態方程式 pV=nRT に従う理想気体と見なせるものとする。ここに、n: モル数 [mol] 、R: 気体定数(R=8.314 J/(mol・K) )である。なお、p: 圧力 [Pa]、V: 体積 [m3]、T: 温度 [K] である。これら、圧力、体積、温度を「気体の状態」と呼ぶ。たとえば、1気圧(=101.3kPa)および 27℃(=27+273 =300 K ) の下で、大きさ5×5×5 [m3] の部屋の中にはn=pV/(RT)=5077 mol の空気が入っている。空気1mol の重さは29グラムであるから、この部屋の中には146kg の空気が入っていることになる。さて、この部屋は密閉されていて、空気の出入りがないとしたとき、気温が40℃まで上昇したとき(状態1から状態2に変化した)、圧力はどうなるであろう?気体の状態方程式からp=nRT/Vより、温度以外は変化がなく温度だけがT1=300K から T2=313K になるのだから、圧力 p2 は(T2/T1)×p1=1.043×101.3kPa=105.7 kPa ( 1.043気圧)に上昇する。
気体の状態変化を使って(温度差の移動する)熱エネルギーから仕事を取り出す。















