連立一次方程式の解とrankの関係を見てみよう。例として未知数の数ｎはｘ、ｙの2つとしよう。つまり、n=2とする。

連立方程式は

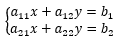
これを行列で表現すると、

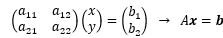
ここに、係数行列を

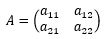
未知数と、定数項をそれぞれ、

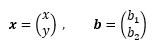
で表した。さらに、拡大係数行列を

とする。

以下に具体的な連立方程式を挙げ、その解について見てみよう。

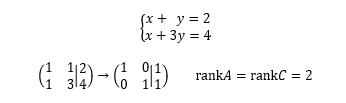
解はｘ＝１，ｙ＝１である。すなわち、2つの直線は1点で交わることを意味し、その交点が解である。

次に、

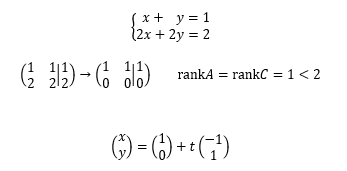
の場合は、ｘ＝１－ｔ、ｙ＝ｔのように任意のｔを選べば解は無数にある。すなわち、式を見ても分かるように2つの直線は全く同じであり、つまり重なっているため、共通する解は無数存在することになる。

次の例は、

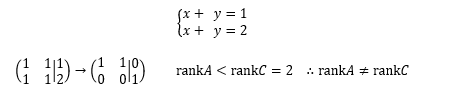
のように、０＝２という不合理なことが起こるので、解は無いことになる。すなわち、2つの直線は平行で交わることが無いために、共通する解は無いことを意味している。

以上まとめると、

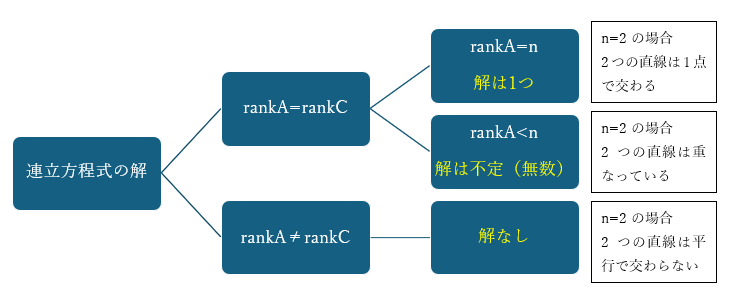
係数行列のrankAと拡大係数行列のrankCが等しいかそうでないかで解があるか無いかが決まり、解がある場合（rankA=rankC）は、rankA=nであれば解はただ一つに決まり、rankA<nの場合は解は無数にあることになる。解が無い場合はrankAとrankCは一致しない。