係数行列のrankAと拡大係数行列のrankCが等しいときで、さらに係数行列のrankAが未知数の数nと等しいときに、解がただ一つに決まることが前項で分かった。この時、逆行列A-1が定義でき、連立方程式の解を次のように書くことが出来る。
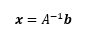
ここに、
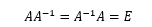
であり、Eは単位行列で2次の正方行列の場合、
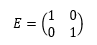
である。
rankA=nの場合、Aが逆行列を持つので、Aは正則であるという。逆にAが正則であればrankA=nであると言える。
また、逆行列は次のようにも表せる。
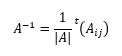
すなわち、逆行列が存在するにはAの行列式が0でないことが必要条件となる。















