例えば、次の2組の一次方程式がともに成り立つ共通するｘ、ｙの組を求めてみよう。これを連立方程式を解くとか、解を求めると表現する。

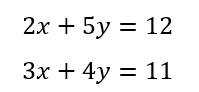
ここで、方程式とは上式のようにｘ、ｙといった未知数を含む等式(=の記号で左辺と右辺が等しいと置いた)で表されるものである。上の例ではその方程式が二つあって、それらを同時に満足するｘ、ｙを求めようというのが2つの方程式を連立させて解くというのである。

１つの方程式を満足する、ｘ、ｙの組み合わせは実は無数にある。方程式の解を縦軸にｙ、横軸にｘをとってプロットすると、直線として表すことができる。これら2つの直線が交わるところ（図では赤の点で表す）。この交わる点は2つの直線上の点であるから、このｘとｙの組み合わせの点が2つの方程式の共通する解である。

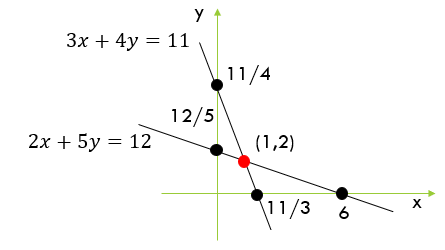
2変数の、つまりｘとｙの、一次方程式では直線となるのでこの2つの直線を含む面内で2つの直線が交われば一つの点のｘ、ｙの組み合わせが解となる。もし2つの直線がある間隔で平行だったら交わる点が無いので解は無いことになる。また、もし2つの直線が同じであったら、重なっているので直線上の全ての点が解となり、解は無数に存在することになる。

つまり、2つの一次方程式によって、１）1つの解がある、２）解が無い、３）解が無数にあるの3通りの場合があることになる。

連立一次方程式の解の求め方には、１）加減法、２）代入法、３）行列を用いた解法、がある。最初の2つは中学校、高校で学ぶので、なじみがあろう。行列を用いたものは大学で学ぶので、これについては別に述べる。