なにやら難しそうな言葉であるが、まず線形性とは何かを下に示す。
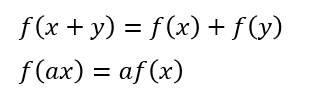
関数がこの関係を満たせば、この関数は線形であるという(線形性を示す)。例えば、f(x)=2xという関数について調べてみよう。まず、f(x+y)=2(x+y)=2x+2y=f(x)+f(y)であるから、最初の関係は満たされることが分かる。2つ目の関係についてはf(ax)=2(ax)=a×(2x)=af(x) となることから、やはりこれも満たすので、f(x)=2xという関数は線形であると言える。
では、f(x)=2x+1という関数はどうであろう?先の関数に1を加えて関数全体を1だけy方向にシフトさせたものである。早速試してみよう。f(x+y)=2(x+y)+1=2x+2y+1=f(x)+f(y)+1 となり、最後の1が残って、上式の最初の関係が満たされないことになる。2つ目の関係はどうであろう? f(ax)=2(ax)+1=a(2x)+1=af(x)+1となり、これも上式の2つ目の関係を満たさないことが分かる。つまり関数f(x)=2x+1は直線ではあるが線形ではない。つまり非線形であるという。
実は原点を通るある傾きの直線だけが線形であり、それ以外の関数はすべて非線形である。非線形の関数の一部を下に示す。
x2, 1/x, x2-8x+12, sin(x), cos(x), log(x), ex,・・・などなど。どれ上式の二つの関係を満たさなので、非線形関数である。
さて、全体の式が非線形の形をしていても、項が線形であれば、線形方程式という。たとえば、
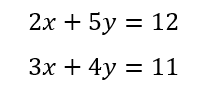
のようなものである。1つ目の式を書き直して、y=(-2/5)x+(12/5)となるので、非線形である。しかし元の式の2x や5y といった項が線形(f(x)=2x , f(y)=5y)であるため、上式の2つはともに線形方程式という。方程式とは、上式の場合を例にとると、未知数であるxとyを含む等式のことをいう。これら2つの方程式をともに満足するxとyを求めることを連立方程式を解くという。
これらの2つの式を連立して解く(解き方については別項目で)と、x=1, y=2の組み合わせを求めることができる。xとyにこれらの値(数字)を代入すると、確かに一つ目の式では2×1+5×2=12になるし、2つ目の式では3×1+4×2=11となって、両方ともに満足する。このような両方の式を満足するxとyの組み合わせを解という。この場合、x=1, y=2が解である。















