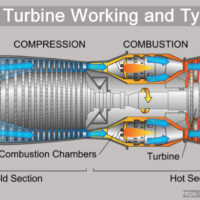
物体が流れの中にある場合には物体表面に作用する圧力を面積分すると物体に作用する圧力による力を求めることができる。その力の流れ方向成分が下流方向を向いていれば、物体を下流側に押す力となるので抗力となる。もしその力が上流側を向いていれば物体を上流側に押す力となるので推力である。静止した流体中をその物体が進むのと上述のことは相対的に同じであるから物体の進行方向に対して逆向きの力となればそれが抗力となる。

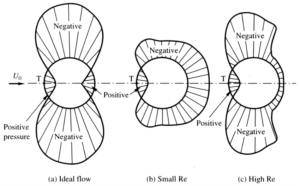
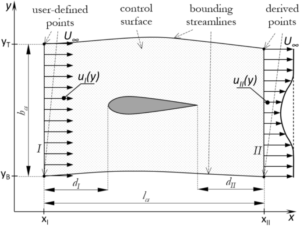
運動量理論から考えると物体の表面力（圧力だけとしよう）が検査体積中の流体の運動量を変化させれば、それが反作用として物体にかかる力となる。抗力の場合は検査体積の出口における流体の運動量は減少したことになる。このことは物体後方の流速が減少することを意味する。この速度減少が見られる物体後方の流れを後流と呼んでいる。

円柱の後流を見ると規則的に並んだ渦の列（カルマン渦列）が見られる。したがってある下流位置で速度を観察すると周期的速度変動が観察されるが、平均して物体後流の速度分布を描けば、物体中心線上で最も低速で外側に向かって滑らかに回復する速度分布となる。

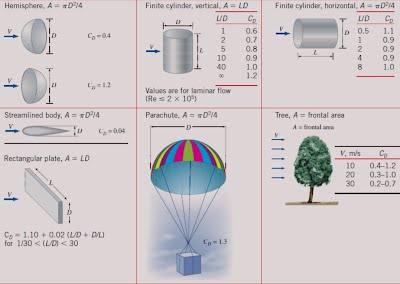
圧力分布を測る、速度分布を測るといったことは大変な作業であるから、予め基本的形状で抗力Dを求め、それと動圧(1/2)ρU² に物体の投影面積Aをかけたものとを係数C_Dで結びつけておけば便利である。各種の物体形状でこのC_Dが求められている。