流れを表す式といえば、ベルヌーイの式だ!というほどこの式は知れ渡っている。しかし、これがどういうものでどう使うのかを説明できる人は少ない。
各部の流れが時間的に変化せず(定常)かつ摩擦等による損失を考えない場合、一本の流線上の2点間で成り立つエネルギー保存則である。ある流体塊(システム)が持っている単位体積当たりのエネルギー(単位を考えると J/m3=Nm/m3=N/m2=Pa となり、圧力の単位となる)は、基準から計った高さ h における位置エネルギー(ρgh)と流速uの運動エネルギー{(1/2)ρu2}、単位体積当たりの内部エネルギー(流体の分子運動に起因する){e (=q+w)}である。なお、q は熱量、w は仕事である。

図に示す一本の流線の1番と2番の位置において、それぞれの番号をサフィクスとして付けて区別する。それぞれの位置でそれらの総和が等しいとすると、次のように書ける。
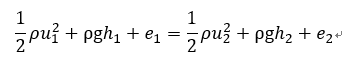
ここで、流れを考えるとき温度は一定だとすると熱力学第一法則から内部エネルギーは外部からなされる仕事 w=W/V= p である。いま、ここで考えている流体塊の体積は単位体積であるから V = 1 m3 であるから、結局、外部からの仕事は圧力で表されることがわかる。これより、一般的にベルヌーイの式は
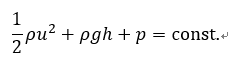
と書ける。第一項を動圧、第二項を静水圧(流体の重さに関わる圧力という意味)、第三項を静圧と呼ぶ。なお、一定(const.)部分を総圧と呼ぶ。
水力学では、各項の圧力を圧力と釣り合う水柱の高さ(水中の水面位置をヘッドと呼ぶ)で表した方が現場で使いやすい。各項を ρg で割って、次のように表す。
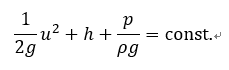
この場合、第一項を速度ヘッド、第二項を位置ヘッド、第三項を圧力ヘッドと呼ぶ。なお、一定(const.)部分を総ヘッドと呼ぶ。
ベルヌーイの式はあくまでも一本の流線上で成り立つものである。なお、各位置を通過する流量を考えるとき、それぞれの位置における面積 A を設定しなければならない。上図のように、流線で囲まれた流管を設定すると、流線で出来た壁を通り抜ける流れが無いと設定できる。すなわち、断面1から流入した流れは断面2から出るという事である。流量 Q はQ=Au であるから、このことを式で表すと
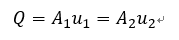
と書ける。これを体積流量一定の式という。
体積流量一定の関係とベルヌーイの式を組み合わせて、いろいろな問題を考えることができる。