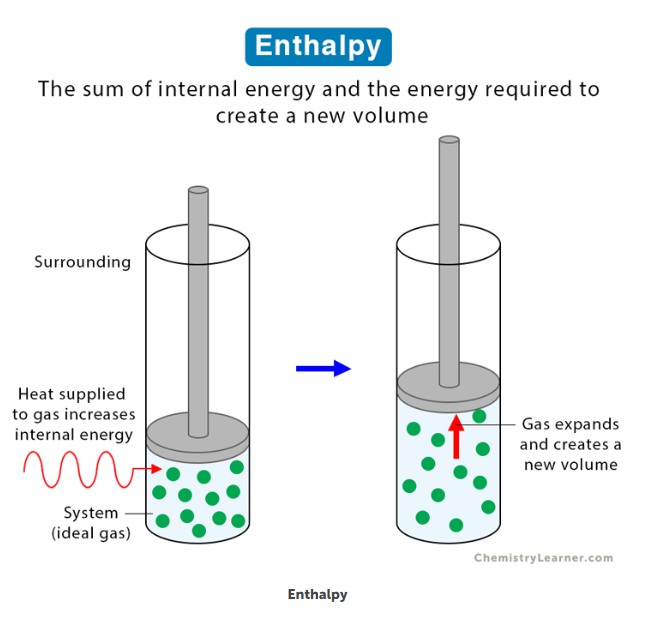
上下に動ける蓋の付いた容器に入った気体を外部から過熱するQと、内部エネルギーUが増加するとともに圧力が上がり蓋を押し上げ外部に仕事 pV をする。外部にする仕事なので -pV である。すなわち、熱力学第一法則よりU=Q+(-pV )であるから、書き直してQ=U+pVと書くと、外部から加えた熱量は気体の内部エネルギーを増加させるとともに外部にpVの仕事ができる能力(エネルギー)に分配されたと考えることができる。つまり外部から加えた熱量は気体のエネルギーの増加になったわけである。この気体のエネルギーU+pVをH=U+pVとかいて、エンタルピーと呼ぶ。内部エネルギー、圧力、体積はすべて状態量なので、エンタルピーも状態量である。すなわち、変化の過程に関係なく、変化前と後の値の差だけで表すことができる。気体の単位質量当たりのエンタルピーを比エンタルピーといって、小文字の h で表す。

蓋つきの容器の場合、蓋には大気圧ｐ＝一定がかかっているとすると、dp=0 なので、dH=dU+d(pV)=dU+pdV+Vdp=dU+pdV である。

状態１から状態2に変わるとき、開いた系における熱力学第一法則から、流動する単位質量の気体の持つエネルギーは(u₂-u₁)+(p₂v₂-p₁v₁)+(1/2)(w₂²–w₁²)+g(z₂-z₁)=q₁₂+w₁₂である。小文字で表したのは単位質量当たりの量であることを表す。斜体の w は流速を表す。また、v は比体積 [m³/kg] を表す。

ここで、エンタルピーの定義から、h=u+pv と書くと、上式は、

(h₂-h₁)+(1/2)(w₂²–w₁²)+g(z₂-z₁)=q₁₂+w₁₂

これに、気体の質量流量を掛けると

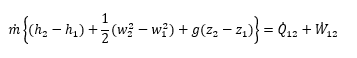
例えば、ある空気圧縮機の質量流量がdm/dt=0.5 kg/sで内部から外部に向けて３ｋWの熱を放出している。入口の空気の比エンタルピーが280　kJ/kg、流速が15　m/s、基準面からの高さが20 m 、出口における比エンタルピーは401　kJ/kg、流速は10 m/s 、基準面からの高さが25 m であるとする。

圧縮機の稼働に必要な動力dW₁₂/dt [W] を上式から求めてみよう。

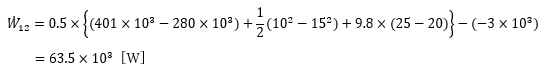
値は正なので、系(システム）は外部から63.5 kWの仕事がなされている。