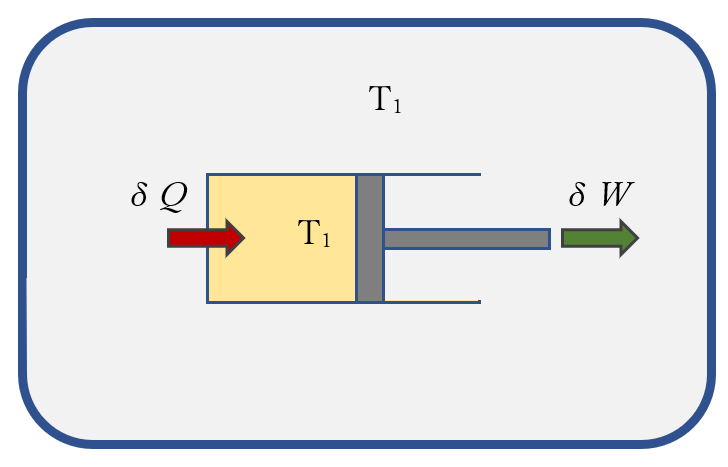
熱力学におけるエントロピーである。巷で言われる分子運動のランダム性や式の形の相似性から派生したエントロピーの概念ではない。熱機関におけるサイクルによって熱エネルギーを使って仕事を取り出す際に、環境に及ぼす影響を表すのに導入されたものである。定義式は
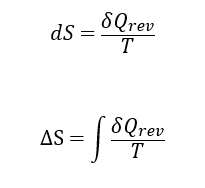
である。Sがエントロピー[J/K] を表し、Qは熱量 [J]、Tは温度 [K] である。上の式は、微小エントロピー変化は温度で表す環境にある過程においてやり取りされた熱量変化の割合を表している。したがって、同じ大きさの熱量の変化があっても環境の温度が高いとき(分母が大きいので)エントロピー変化は小さく、その逆に低温環境であればエントロピー変化は大きくなる。環境は広い空間なのでその熱容量は大きく、そこに熱量が投入されても温度変化は無い、つまり等温であることが暗黙的に仮定されている。したがってエントロピーは等温状態で熱量を可逆的に受け渡しするときの状態変化を表している。言い換えれば、熱量が環境にどの程度影響したのかを表す指標である。ΔS は温度 T が一定のもとある状態 1 から別の状態 2 に移行したときのエントロピー変化 ΔS = S2-S1 を表したものである。じつは完全に等温であると熱量は移動しない。なぜなら、熱量 Q の定義は Q=mcΔT であるからである。ΔTは温度差を表すので、等温では ΔT=0 であるから、Q=0 となって、熱量は移動しないことになる。つまり、等温では熱の受け渡しができないのである。そこで導入されたのが準静的過程とよばれる方法である。ゆっくりと時間をかけてほぼ等温とみなせる程度のわずかな温度差ΔTをつけて熱エネルギーを移動させるのである。
等温変化の場合は、気体の状態方程式 pV=nRT より、T=T1 = 一定であるから、pV=nRT1=一定である。すなわち圧力 p と体積 V は反比例の関係にある。ピストンーシリンダ内に入っている気体(システム)がピストンの移動で行う外部への仕事は δW=-pdV である。状態方程式で表せる関係 p=nRT1/V をこれに代入すると、δW=-(nRT1/V )dV と表わせる。これを状態1から状態2へ積分することで仕事が求められる。
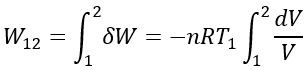
したがって、
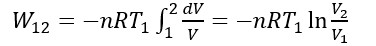
状態1の時の体積 V1 と状態2の時の体積 V2 の比のログで外部への仕事を表すことができる。ところで、システム内の内部エネルギー変化 ΔU は等温変化では ΔU= 0 である。したがって、熱力学第一法則 ΔU=Q12+W12 より、Q12=-W12 であることがわかる。これに上式の関係を代入すると、
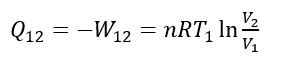
と表わされる。つまり、等温状態でシステムが外部に仕事をすると(体積が膨張)、環境からシステムに熱量Q12が入ってくることを意味している。周囲の環境とシステムとの間に温度に差を付けなくても外部に仕事をすることで熱量をシステムに取り入れることができる。見方を変えれば周囲から入った熱量でそれと同等のエネルギーの仕事を環境にしたと言っても良い。図に示すように、まるで注射器のピストンを引くことで周囲環境から熱エネルギーを吸い取ったというイメージである。逆に状態2から状態1に等温で変化させれば周囲に熱量を放出することもでき、周囲に影響が残ることなく元通りに戻すこともできる。このような変化をさせられる過程を可逆過程という。さて、システムのエントロピー変化 ΔS は上の関係から、
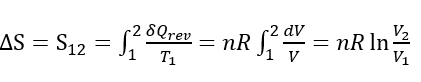
と求められる。この場合のエントロピーは状態1と状態2における値の差 S12=S2-S1 として表すことができるので、最初に示したエントロピーの定義式においてdSと表わしたのである。
エントロピー変化を体積変化として表したが、pV=一定の関係から、圧力の変化としても表すことができる。すなわち p1V1=p2V2 より、
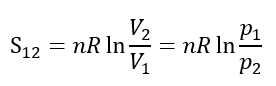
である。