未知数の数n=2の場合、すなわち、未知数がx1, x2 の二つの場合の連立方程式を拡大係数行列を使って解く。例として、
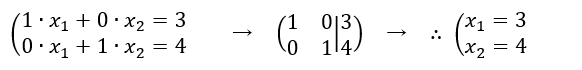
これをグラフで書いてみると、
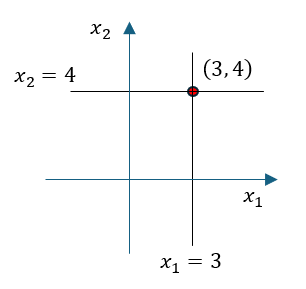
すなわち、二つの未知数を持つ方程式というのは直線を表すので連立方程式を解くということは、この場合、x2軸に平行な直線x1=3 と、x1軸に平行な直線x2=4 が交わる点(両方の直線に共通する点)を求めることに他ならない。この例ではたまたま二つの直線がそれぞれ軸に平行な直線であったに過ぎない。
同様に他の例も見てみよう。異なる傾きを持った直線が1点で交わる場合、
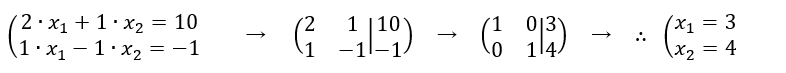
グラフで表すと、
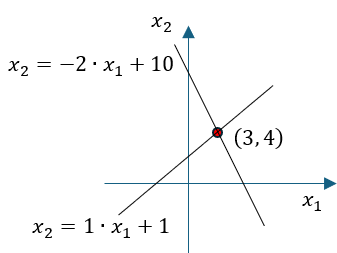
3つの直線が1点で交わる場合の例として、
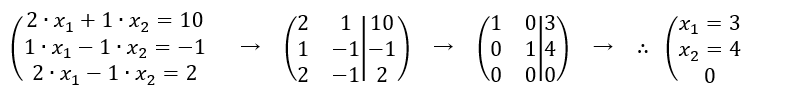
グラフでは、
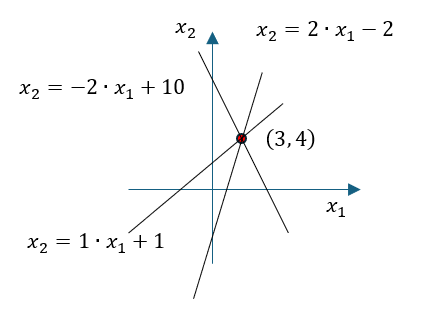
となる。
今係数行列A や階段行列に着目してみよう。

影を付けた部分が階段状になっているので階段行列という。最後の階段行列では最後の行ベクトルがすべて0なのでこれを段数には含めない。この段数を階数(rank)という。上の例ではどれもrankは2である。
上述の3つの例におけるrankと未知数の数nを見てみると、どれも
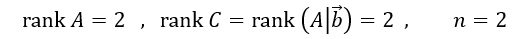
である。つまり、

の関係にあるとき、階数(rank)と未知数の数が等しいとき、1点で交わる。すなわち、解はただ1つであることが分かる。
















