シリンダ内に閉じ込めた気体を使って、仕事を取り出すためには熱エネルギーを与えて気体を膨張させればよかった。しかしこれでは一度膨張させたら一回仕事できるだけである。連続的に仕事を取り出すためにいったん膨張した気体を元に戻して再び膨張させるという繰り返し動作ーこれをサイクルというーを考えねばならない。気体の状態を元に戻すのに取り出した仕事をこれに使うのであれば元の木阿弥状態となるので、元に戻す仕事を少なくして、差し引き外部への仕事となるようにする工夫が必要である。
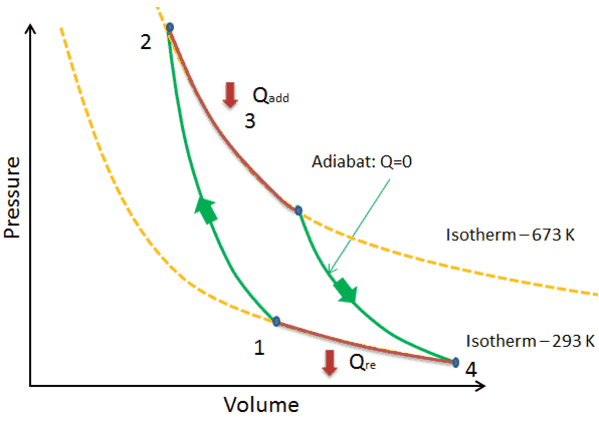
気体の状態方程式 pV=nRT を使って、仕事W [J]を取り出すことを考えてみよう。ここで、p: 圧力 [Pa]、V: 体積 [ m3]、n:モル数 [mol] 、T: 温度 [K]、R: 気体定数 ( = 8.31 [J/(mol・K)]である。気体の状態方程式の左辺 pV [N/m2* m3=Nm=J] は仕事そのものである。したがって、p-V線図の変化曲線の下側の面積(p×V)が仕事を表す。サイクルを描く曲線にそって積分すると差し引きループの内側面積が仕事を表す。カルノーサイクルは与えられた温度差においてこの面積が最大となるサイクルである。
上図でいえば1→2: 断熱圧縮、2→3: 等温膨張、3→4: 断熱膨張、4→1: 等温圧縮のそれぞれの過程である。等温膨張過程で外部から熱量Qaddを受け取り、等温圧縮過程でQreを外部に排出する。それらの差 Qadd-Qreが外部に成す仕事Wとして取り出せる。したがって、熱効率 η は次のように表せる。
η = W/Qadd = ( Qadd – Qre ) / Qadd = 1- ( Qre/Qadd) = 1-(TL/TH)
排熱する際の周囲温度 TL が低い方が効率は良い、または周囲温度が同じであれば高温源の温度 TH が高い方が効率は良いことがわかる。なお、等温で熱量のやり取りをするのは無限の時間をかけて(準静的過程=可逆過程)、ゆっくりと膨張させるとかゆっくり圧縮してシステム内部と外界の熱量のやり取りをさせるので、非現実的である点で理想サイクルである。したがって、現実には同じ温度差で取り出せる仕事はカルノーサイクルを超えることはできない。