水中で物体が加速運動する時、水を押し退けるのに水に力を作用させた結果、水からの反力を物体が受けることになる。押し退ける体積はその物体がその空間に移動した分であるから、単純に考えればその物体の体積である。それをVとすると押し退けられた水の質量はρVである。この水に物体が加速 a するのに必要な力で水も動かすわけであるから、水に与えた力はρVaである。これと同じ大きさの反力を水から受けるので質量Mの物体の運動方程式は推力をTと書くと、
Ma=T-D-ρVa
ここに、Dはその時の速度に応じた形状抵抗である。この式を書き換えて
(M+ρV)a=T-D
となる。ここでρVをM’と書くと、運動方程式は (M+M’)a=T-D のように表せる。このM’ が付加質量と呼ばれるものである。
大抵の場合は一定速度で運動する定常状態を扱うので、この付加質量は現れないのである。一定速度で移動する物体の推力は抵抗と釣り合う分だけである。それより大きな推力を出した途端に加速運動となるので付加質量を考慮しなくてはならなくなる。もちろん減速時にも考慮する。
物体の体積と同じ水の質量が付加質量分となると書いたのは便宜上であって、実は物体の運動によって影響を受ける水の量はそう単純には見積もれない。水には粘性があって、物体の運動が周囲にどのくらいの範囲まで伝わるのかに依存するからである。影響の範囲を明確に決められないので付加質量も見積もれなくなる。そのため、水を非粘性として理想流体として扱うことにして、ポテンシャル流れで基本的形状の付加質量を求めている(表参照)。
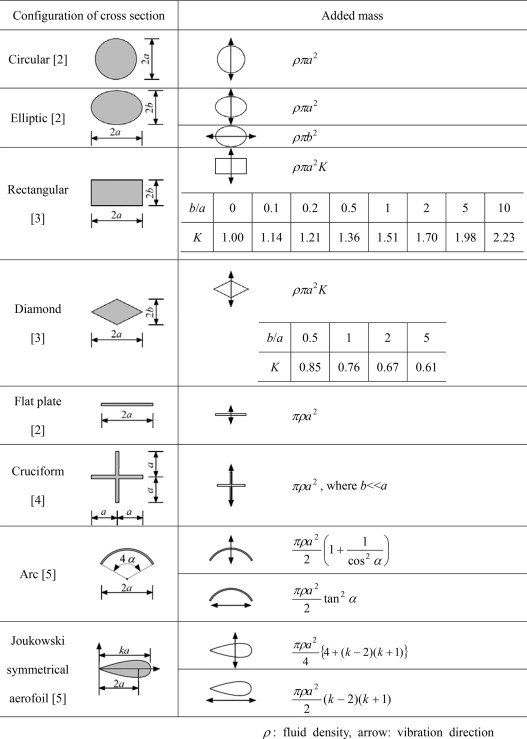
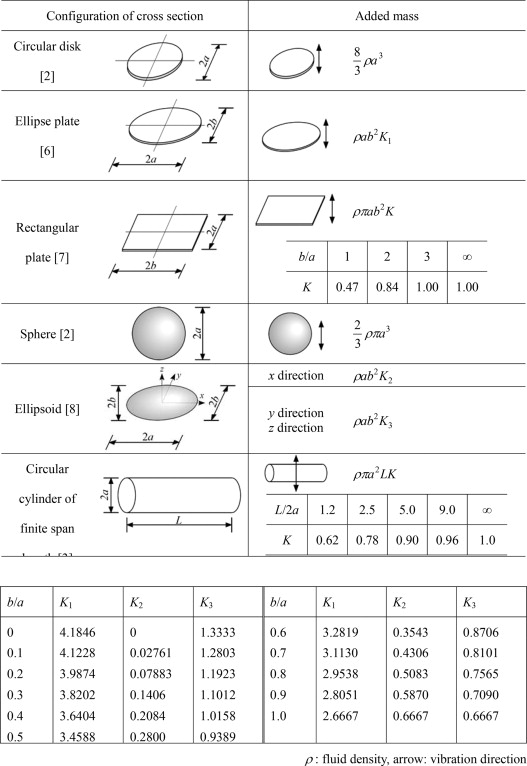
円柱の場合、付加質量分の体積は単位長さあたりの体積と同じであることがわかる。また、3次元物体である例えば球体では、球の体積の半分であることがわかる。これらはあくまでも粘性を考慮していないので、実際よりは小さく評価している。しかし、レイノルズ数の大きな場合では粘性の影響は小さいので、この非粘性で見積もったものとして差し支えない。
この付加質量を考慮しなければならない事例として、波にさらされる海洋構造物にかかる力の見積、大型船の加速減速時の推力の見積り、などである。気泡のような軽い物の運動には付加質量の方がそのものの質量より大きい。
空気中でも加速運動時には付加質量分を考慮する必要はあるが、空気の密度が小さいので普通は無視できるが、気球や飛行船のようなものでは考慮が必要となる。
水面を掌でゆっくり押すとズブズブと容易に手は水中に入るが、思いっきり叩くとパーンとまるで固体を叩いたかのような感じを受ける。手のひらの大きさは同じだが、加速度が大きく異なるので付加質量分の反力が手の衝撃として返ってくるためである。この経験をすると付加質量の重要性がわかる。
















