閉鎖系の熱力学第一法則は次のように書ける。なお、Uは内部エネルギー、Qは熱量、Wは仕事を表す。

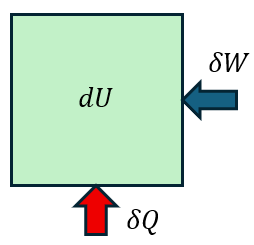
すなわち、系に対して外界から熱量δQと仕事δWが加えられた時、系の内部エネルギー変化dUはそれらの和として与えられるということである。言い換えれば、系の内部エネルギーは外界から加えられる熱量と仕事によって変化するということである。閉鎖系であるから、系内の質量は一定である。
等積過程において、外界から熱量を加えたときのことについて考えてみよう。つまり体積が変化しない容器の中と閉じ込められた気体の状態がどのように変化するのかを考える。式(1)のδWは0であるから、式(1)より、
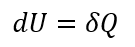
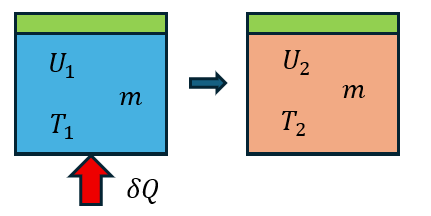
外界から加えた熱量は系の内部エネルギーを変化させる。ここにTは系内の温度であり、mは系内の質量である。
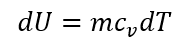
であるから、状態がサフィックスの1で表す平衡状態からサフィックスの2で表す平衡状態へ変化したとして、両辺を積分すると、
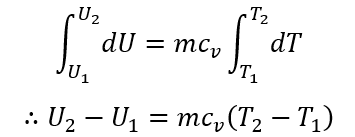
ここに、cvは定積比熱であり、単位は[J/(kg・K)]である。すなわち、内部エネルギーの変化は温度の変化として計測することが出来る。
なお、系内部の圧力は気体の状態方程式から、
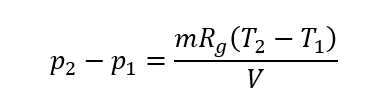
であり、気体を空気とすると、気体定数Rg=286.99 [J/(kg・K)]である。つまり、温度が上昇する分、圧力は高くなる。
等圧過程ではどうなるのか?それぞれの状態で系内部の圧力は、外部から受ける圧力と等しいのでp1=p2=paである。また、質量は一定でmである。
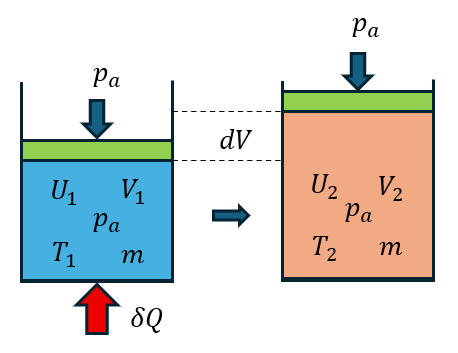
圧力を一定にするためには、図のように蓋が上下に動けるようにすると、系内の圧力は1と2の平衡状態では外部の圧力と釣り合っていることになる。また、熱量を加えると、系の体積は膨張し、系は外界に対して仕事をする。すなわち、加えられた熱量(熱エネルギー)は系の内部エネルギー増加dUと外界にする仕事(pdV)に分配されるのである。そこで、次のような量を定義する。
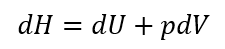
このHをエンタルピーと呼ぶ。
ここで、p=paであるから、pdV=padVであり、系が外界に対して行った膨張仕事であるので、padV=-δWと書ける。これと熱力学第一法則の式(1)の関係を式(3)に代入すると、
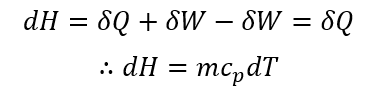
すなわち、外部から加えた熱量が系内部のHの状態変化として表されたことになる。したがって、
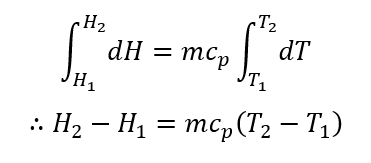
ここに、cpは定圧比熱であり、単位は[J/(kg・K)]。このHをエンタルピーと呼んで、内部エネルギーの変化と仕事を加えたエネルギーと定義すると、圧力が一定の環境における系のエネルギー変化(エントロピー変化)を状態量として扱うことが出来るのである。等圧過程において、系に出入りする熱量の変化は系のエンタルピー変化に等しいと言える。
ちなみに、等圧下で行われる化学反応においてエンタルピーが増加するのは吸熱反応であり、エンタルピーが減少するのは発熱反応である。
















