未知数n=2の連立方程式を例に見ていこう。
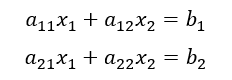
で表される、連立方程式を行列を使って表すと、
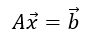
である。ここに、
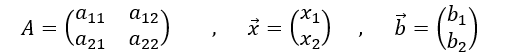
いまこの場合、rank A =2であれば解はただ一つ存在し、先の項目で見てきたように、係数行列Aの逆行列が存在する。逆行列は、
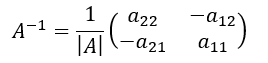
で表される。ここに |A| は行列式であり、次のように表される。
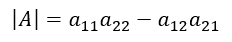
逆行列の表現においてこの行列式は分母にあるので、|A|=0では逆行列の値が求められず、したがって、逆行列が存在するためには
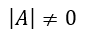
でなければならない。
係数行列Aが正則であれば(Aの逆行列が存在すれば)、言い換えればAの行列式が0でなければ、解はただ一つに定まる。
連立方程式の2つの直線は一点で交わる。
例を示そう。
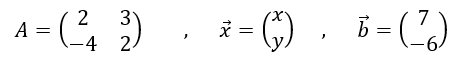
の場合、行列式は
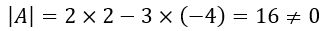
であるから、解はただ一つ存在する。
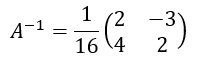
より解を求めると、
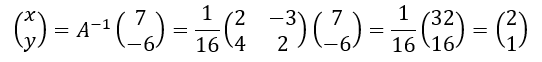
したがって、2つの直線は点(2,1)で交わる。なお、rankを確認すると、rank A=2となっている。















