一つの平面で二つのベクトルa, b を使って、任意のベクトルpを表わそう。ベクトルa, bは同一直線上に無いとする。そうでないと一つの面を決められないからである。つまり、二つのベクトルはある角度をなしていて、このような関係を一次独立という。

p=ma+nb

m,nは任意の値である。つまり、ベクトルaをm倍し、ベクトルbをn倍して足し合わせてベクトルpを作ることになる。ベクトルpはベクトルmaとnbをそれぞれ辺の長さとする平行四辺形の対角線として表すのである。

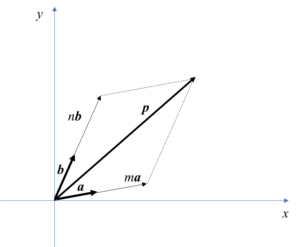
ベクトルを成分表示してみよう。つまり、平面におけるベクトルの矢印の頭をxとyの座標で表したものである。矢印の始点は原点(0,0)とする。ベクトルaはa=(a_x, a_y), ベクトルbはb=(b_x, b_y)である。同様にベクトルpはp=(p_x, p_y)であり、先ほどのp=ma+nbの関係から(p_x, p_y)=(ma_x+nb_x , ma_y+nb_y)である。

例題１）具体的にp=(10, 8)としよう。a=(2,1) , b=(1,2) とするとき、mとnを求めよ。x, yそれぞれの成分の関係から、2m+n=10, m+2n=8 の関係を得る。したがって、mとnに関する連立一次方程式となるので、m=4, n=2と求められる。したがって、p=4a+2bと表わされる。

ベクトルは2行1列の行列として表される。すなわち

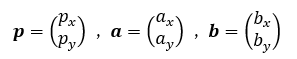
である。したがって、p=ma+nbの関係は

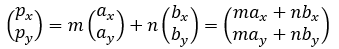
と表わされる。

先ほどの連立方程式　2m+n=10とm+2n=8 の関係も行列で表すと、

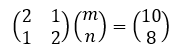
である。いま係数行列をAで表すと、

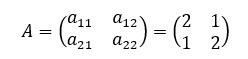
であるから、行列式|A|=3となり、0ではないので、逆行列A^-1が存在する。逆行列は、

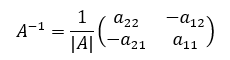
であるから、解は

と求められる。もちろんこれでもいいのであるが、クラメルの公式を使って解を求めてみよう。

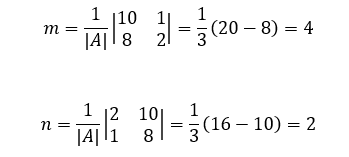
もちろん同じ解を求められる。

例題２）さて先ほどは、ベクトルaとbを与えて、係数ｍとnを調整してベクトルpを決定したが、今度はベクトルpを決定するために係数m=3, n=2 としてベクトルaとbを逆に求めてみよう。

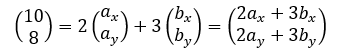
であるから、

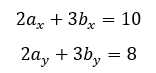
上式では未知数が4つもあるのに方程式が2つしかないので、解を求められない。

そこで例えば、a_x=2 , a_y=1とすると、b_x=2 , b_y=2と求められる。つまり一つのベクトルを仮定すると、他のベクトルを決定できるのである。もちろん、他の値にすればたとえば　a_x=1 , a_y=2とすると、b_x=8/3 , b_y=4/3と求められる。つまりこの場合、ベクトルpを決めるベクトルaとbの組み合わせは無数にあるということになる。重要なのは解が無いのではなく、自由に決められるのである。

考察　：　例題1）はいわば高校までの問題形式であり、与えられた部品(ベクトルa, b )であるもの（ベクトルp）を調整して作りなさいというものであったので、部品が決められている以上答えは一つしかなかった。これに対して、例題2)の場合は、与えられた条件（m と n）のもと目標のベクトルpを作れというものであった。つまり条件さえ満足していれば、設計者の好きな部品（ベクトルa, b）を持ってきて作れるのである。この時、エンジニアとして大きな決断を迫られることになる。つまり、まず一個の部品(例えばベクトルa）を今までの経験と嗜好でえいやっ！と決めなければならないのである。その時、他の部品(ベクトルb）が手に入るもの、もしくは自分の考えに沿ったものであれば良し、そうでなければ決め直さねばならないのである。設計者は常にこの苦しみを背負うことになるのである。自由に決められる、なんでもオーケーという自由は辛いのである。例えば先ほどのa_x=2 , a_y=1とすると、b_x=2 , b_y=2となるのが良いのか、　a_x=1 , a_y=2とすると、b_x=8/3 , b_y=4/3となるのが良いのか判断しなければならない。後者のケースは3で割るということになるので、割り切れない気持ちとなる（洒落）から、採用しないとか、こういった葛藤を経て物の設計は行われる。ここで大事なのは、目的であるベクトルpを設定しない限りこれらの設計はできないので、何を作るのか？何をどうしたいのか？という目的をはっきりさせることがまずは重要な事である。