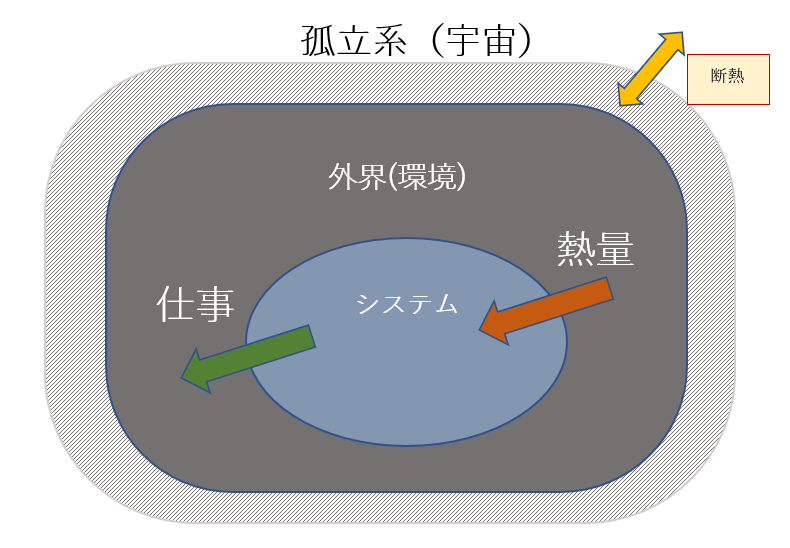
システム内の温度や圧力が常に外部と同じとみなせる状態でシステムが変化するとき、準静的変化という。システムの状態が「非常にゆっくりと変化する」と表現される。

準静的変化において理想サイクルのカルノーサイクルが等温変化で膨張するとき、外部の温度とサイクル内の温度は同じとみなされるにもかかわらず、熱量が外部からサイクル内に入る。これは熱量の定義 Q=mcΔT と矛盾する。つまりΔT=0なのに熱量がシステム内に入るのはおかしいことになる。そこで、システム内と外部との間にわずかに温度差を付けて熱量を取り込み、その熱量が入ることでシステム内の温度が元に戻って一定温度を保つと考えるのである。そのためごく僅かだけ温度差を付けてゆっくりと熱量を取り込むのである。温度差を付けるためにカルノーサイクルでは外部に向かって体積を膨張させ仕事をし、その分で温度をわずかだけ低下させるのである。このわずかな温度差で熱量を取り込む。熱量が入ればシステムの温度は元に戻る。このように温度を一定に保って変化させるのを等温変化という。

等温変化における気体の状態方程式は pV=nRT₁= 一定である。システムが外部にわずかに膨張 dV して成す微小仕事 δW は δW=-pdV であるから、状態１から状態2に変化するときの仕事 W₁₂ は、

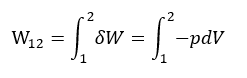
と表わされる。等温変化における気体の状態方程式の p をこれに代入すると、

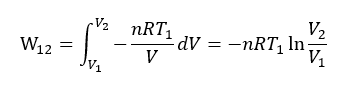
システム内の内部エネルギー変化 ΔU は温度一定なので、ΔU=0 である。したがって、熱力学第一法則 ΔU=Q₁₂+W₁₂ から、Q₁₂=-W₁₂ である。つまり、等温変化では外部の仕事によって熱量が可逆的にシステム内に取り込まれる。その熱量は、

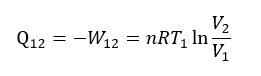
この時のシステム内のエントロピー変化は状態1と状態2におけるエントロピーの差として表されるので、 ΔS_sys=S₂-S₁ である。また、 ΔS_sys=Q₁₂/T₁ であるから、

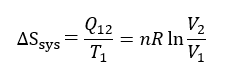
システムのエントロピーは増加することがわかる。なお、環境とシステムを内包した系が孤立系であれば断熱（δQ=0）であるから、孤立系全体では ΔS＝０ である。すなわち環境のエントロピー変化を ΔS_out と表わすと、ΔS=ΔS_sys + ΔS_out =0 であるから、 ΔS_out は、

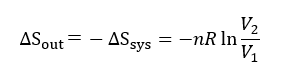
環境のエントロピーは減少する。