有限の熱容量Qを持つ温度T_Hの高温熱源が周囲環境の温度T_Lの低温度熱源との間でどのくらいの仕事ができるのか考えてみよう。例えばT_H＝600K(327℃)に加熱された質量500kgの石が環境温度T_L=300K(27℃)に置かれているとしよう。環境はこの石で温められるが広いので温度の変化は無視できるものとする。つまり、27℃のままであるとする。

この石の温度は徐々に下がっていき、ついには周囲の温度にまで冷えることになる。これは経験的に「そうなる」と言える変化である。これを自発的変化といい、自然に放っておくと自然とそのような状態になるというものである。つまり手を加えない限り熱いものは冷える方向に向かう。この温度差で、移動するエネルギーを熱エネルギー(熱容量)と言い、物体の質量mと比熱cと温度差ΔT=(T_H-T_L)を用いて、次のように定義される。

Q=mcΔT=mc(T_H-T_L)

これがこの温度差でこの物体が持っている全熱エネルギーである。このまま放っておけばこの熱エネルギーは物体の温度が周囲環境温度になるまで環境に移動して、物体は冷えていく。環境の温度となった状態を熱的平衡状態という。

さて、この熱エネルギーをカルノーサイクルエンジンを使って仕事にどれだけ変換できるかを見積もってみよう。ある温度Tと環境温度T_Lの間で取り出せる微小仕事をδW、微小熱量をδQとしてカルノーエンジンの熱効率をη_c (=1-T_L/T)とする。物体温度Tの時に取り出せる微小仕事は、

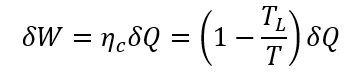
と表わせる。ここで、物体から流れ出ていく（マイナス符号でそのことを表す）熱エネルギー(熱量)はδQ=-mc dTであるから、これを上式に代入すると、

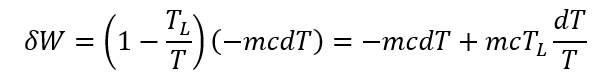
となる。両辺を初期状態1の温度T_Hから最終状態2の周囲温度T_Lまで積分すると、

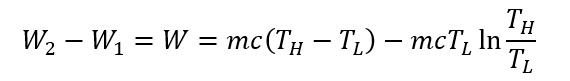
となる。すなわちこの加熱された石を使ってカルノーエンジンに熱量をつぎ込めば、仕事Wができるのである。ここで、右辺第一項は先に示したこの加熱された石が持っている全熱エネルギーである。右辺第二項が仕事に使えないエネルギーを表していて、これをアネルギーと呼んでいる。全熱エネルギーからアネルギーを差し引いた分が仕事に使えるエネルギーであり、これをエクセルギーと呼ぶ。この式から、理想的なカルノーサイクルを使っても石が持っている全熱エネルギーの全てを仕事に変えることができないことを表している。上式を言葉で書き換えれば、

（エクセルギー）＝（全熱エネルギー）ー（アネルギー）

である。もしくは

（全熱エネルギー）＝（エクセルギー）＋（アネルギー）

と表わせる。カルノーエンジンで可逆的に仕事を取り出しているので、エクセルギーはこの熱源から取り出し得る最大仕事となる。

冒頭で与えた条件で、熱せられた石（比熱を0.8 kJ/(kg・K)としよう）の全エネルギーとエクセルギーを求めてみよう。

全エネルギーは　Q=500×0.8×10³×(600-300)=120×10⁶ J =120 MJ

エクセルギーは　W=120 MJ-500×0.8×10³×300×ln(600/300) = 120 MJ – 83 MJ = 37 MJ

となる。