コマの様に円盤が回転するとき、回転中心から r 離れた点の円周の接線方向速度（周速度）を v とする。回転の角速度を ω [rad/s]とするとき、それらの関係は次のように表せる。なお本来ベクトル量であるが、ここでは簡単に頭につける矢印を省いて表す。

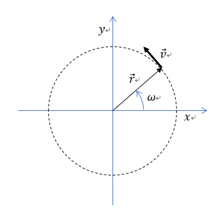
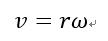
なお、ω というのは1秒間に回った角度を表し、この時の角度を°(度）の代わりにrad（ラジアンと読む）で表す。したがって単位は [ rad/s ] である。１秒間に移動する距離のことを速度というのに対して、１秒間に回った角度のことを角速度という。度（°）とラジアンの換算は、一回転360度が2πに相当する。一般的に回転数を1分間にｎ 回転したとするとn [rpm] と表す。工学的には1秒間に換算して使うので、1分は60秒であるので、これをn/60 [rps]で表す。また、1回転というのは角度でいうと360度、すなわち2π ラジアンであるので、n 回転というのは2πn ラジアン回ったことになる。したがって、ωをnを使って書き換えると、

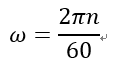
と表現できる。これを使って半径 r のところの周速度 v は次のように書ける。

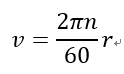
したがって、 r 位置の周速度は回転数 n [rpm] と回転半径 r [m] に比例する。