質量とはシステム（系）の動き易さ・動き難さを表す指標である。同じ力を加えたときそのシステムが大きな加速を得たとすると質量は小さい、逆に小さな加速しか得られないとすると質量は大きいと表現する。言い換えればそのシステムの性質を表す表現の一つである。したがって、普通に観測する流体のシステムであればその性質は変わらないと考えられる。レイノルズの輸送理論式において、Bを質量だとすると、B_sysは短い時間内で変化しないとすると、

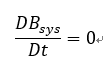
である。また、オイラーの観測窓（CV）も時間的に変形しないとすると、

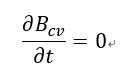
であるから、レイノルズの輸送理論式は結局次の様にあらわされる。

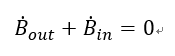
ここで、CVに入る・出るということを数学的にどのように表すのかを次のように取り決める。ものを取り囲んでいる面の方向を面要素に垂直外側に向けた単位長さのベクトル(矢印）、これを法線ベクトルと呼ぶ、で表す。CVが四角で出来ているとすれば面と法線ベクトルの関係は次の図の様に示すことができる

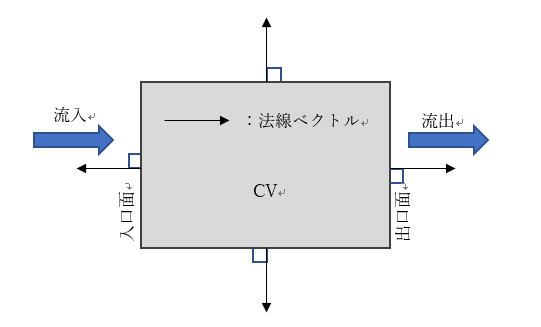
入口に流入する方向が右向きであるとすると、入口面の法線ベクトルの方向は逆の左向きになっている。したがって、入口に入るという事をマイナスの記号で表す。これに対して、出口では法線ベクトルの方向と流出する方向が同じであるから、このことをプラスの記号で表す。これを用いて上式におけるBのサフィックスであるout と in のかわりにプラスとマイナスで表すと次のように書ける。

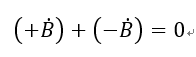
マイナスの項を右辺に移項すると、結局

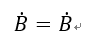
となり、CVから出ていく質量とCVに入ってくる質量は同じという事が導かれる。上図の上下の面から漏れたり入ってきたりしないという事は暗黙の了解となっているため（流線の一部となっている仮定）、このようなことが言えるのである。これを質量流量一定の法則または質量保存則と呼んでいる。

入口面積をA₁、流入速度u₁、出口面積をA₂、流出速度u₂、とし、流体の密度をρとすると、質量保存則は

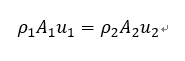
と書け、ここで密度は一定であるとすると、両辺のρは約分されて、

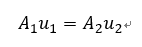
と書くことができる。このAuは底面積Aに単位時間当たりの高さuをかけたものは単位時間当たりの体積を表すので、これを体積流量と呼ぶ。この式を体積流量一定の式という。