f(x)とx=a,b, およびy=0 (x軸）で囲まれた図形をy軸周りに回転させるときにできる立体の体積Vを求めよう。

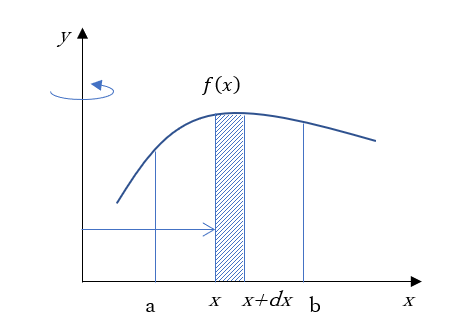
図のようにy軸から計ってxの位置にdxの幅を持つ短冊が回転するものとする。短冊の高さはf(x)である。回転すると円環となるが、これを一周切り取って開くと下に示すような図となる。

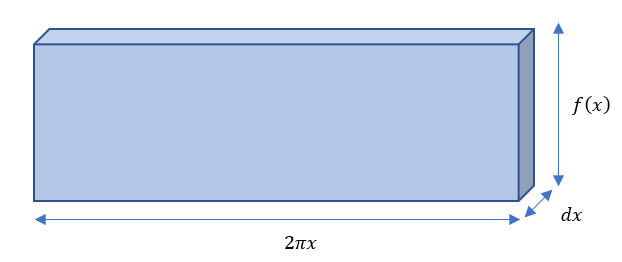
個の薄い直方体の体積dVは

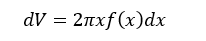
であるから、これをaからbまで積分すると、回転体の体積が求まることになる。したがって、

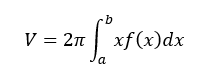
である。ここで、重心のｘ座標が次のように表されることを思い出そう。

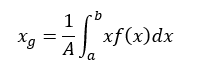
ここにAは断面図形の面積である。これを先の体積の式に代入すると、

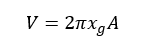
である。なお、2πx_gは、重心のｘ座標までを半径とした円の円周を表す。つまり、重心の一周する距離（周長）に断面の面積を掛けると回転体の体積が求まるのである。

団扇の柄を持った位置から重心(ほぼ中心）までの距離を長くすると、団扇の面積が同じにもかかわらず、動かせる空気の体積量は多いということになる。これは魚の尾ひれ形状とその運動に通じるものである。