ある図形があって、その重心の座標を(x_g, y_g)とする。また、あるｘ位置におけるｙ方向の幅をh(x)とし、同様にあるｙ位置における横方向の幅をk(y)とする。

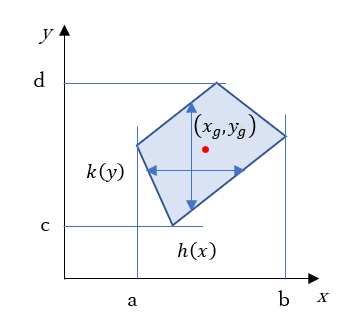
重心というのはその点におけるモーメントが0となる点である。つまり重心点で図のような板を水平に支えると傾くことなくバランスして水平を保っている。たとえば、x_gまわりのモーメントは距離×重さである。重さというのは微小体積に密度を掛けたものとして表す。微小体積は奥行き方向に単位長さ1をとってh(x)dx×1である。これに密度ρ（=1とする）を掛ける。x_gからのxまでの距離は(x-x_g)であるから、したがってx_gまわりのx方向のモーメントは(x-x_g)h(x)dxと表わされる。これを図のx方向の範囲積分した結果が0となるxgが重心ということになる。したがって、

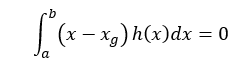
と表わされる。これを展開すると、

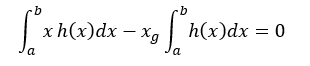
ここで、

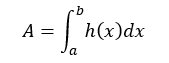
Aはこの図の面積であることを考慮すると、上式より重心のｘ座標 x_gは、次のように表せる。

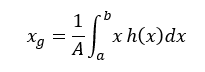
y_gについても上と同様に、

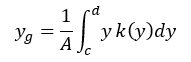
と求められる。