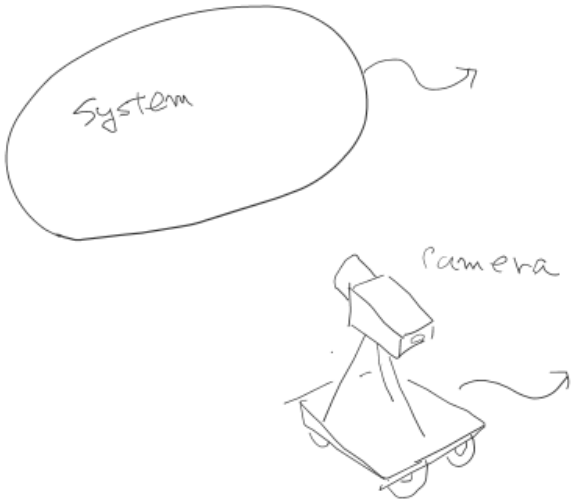
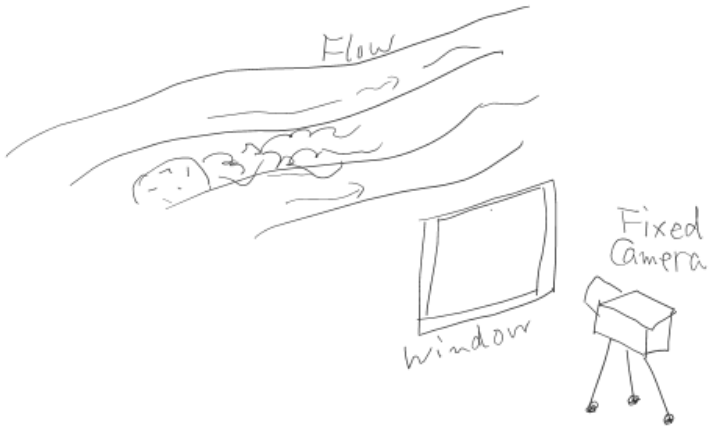
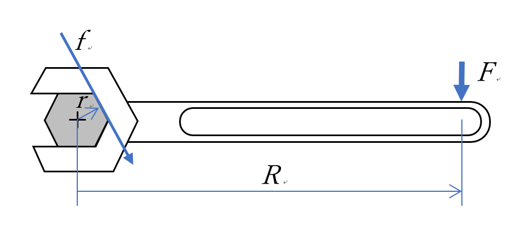
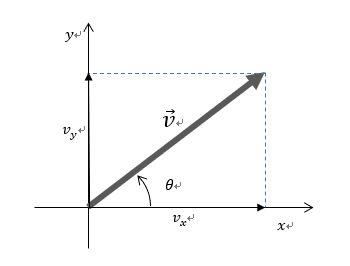
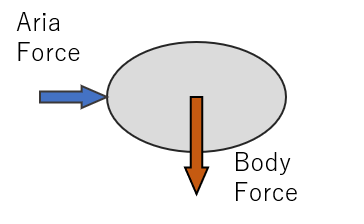
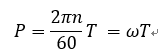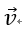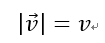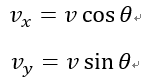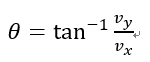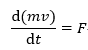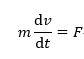ラグランジュ的観察しているシステムがオイラー的観察窓に入って、ぴったりとはまり込んで、出ていく短い時間のオイラー的観測結果が一致したとするときを表すものであり、以下のレイノルズ輸送定理式となる。

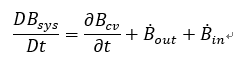
ここで、B_sys はシステムのある量、例えば密度、速度、運動量などである。D/Dtは実質微分と呼ばれるもので、

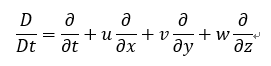
と書ける。流体のシステムBが移動中に時間と場所で受ける変化を表すものである。ここに、u,v,w はx,y,z 方向の速度成分である。固体の運動のように場所によって変化を受けなければ時間微分だけが残る。流体は容易に変形できるので、運動中、例えばすぼまった管を通り抜けるとき長細くなるであろう。そのとき長くなった部位は長くなるという変化を受け、B が速度の場合と加速を受けることになる。そのため、その場所による加速度を表すことになる。

レイノルズ輸送定理式の右辺のB_cv はオイラーの観察窓と呼ばれる容器（コントロールボリュームと呼ばれCVで表す）の中のある量、例えば密度、速度、運動量などである。したがって、右辺第一項はそのCV中のBの時間変化である。定常の場合は時間的に変化しないのでこの項は０となる。

右辺の

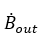
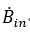
は、それぞれCVから出る B の時間変化（ドットで表している）と入ってくるBの時間変化を表している。この時、入ると出るを符号マイナス、プラスで表す。

たとえば、CVに1秒間に10m³の量の水が入ってきて、8m³出ていったとする。その時入る量にマイナスを付け、-10 m³/sと表わし、流出する量に+8m³/sと表わす。

この例ではBは体積を表す。右辺の実質微分ではシステムの体積が観察時間内に変化しなかったとすると、右辺は0である。したがって、レイノルズ輸送定理式にこれらを代入すると、

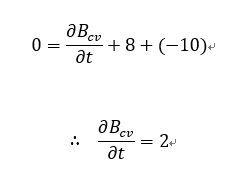
となる。すなわちCVの体積の時間変化率は2m³/s であるから、一秒間に2m³づつ増えていくことを表している。

流れを観察する（数学的取り扱いのできる）方法は2つある。一つは流れの一部にマーカーを付けて、これをシステムと呼び、その運動をシステムの動きと同調して動きながら観察する方法、これをラグランジュ的観察と呼ぶ。もう一つは、固定した位置にある窓を通して観察し、そこを出入りする変化を調べる方法、これをオイラー的観察と呼ぶ。

ラグランジュ的観察では空に浮かんだ一塊の雲がどのように流れていくのかな？と観ているやり方である。これはあたかも投げられたボールを観て、放物運動しているなと理解するやり方と同じであるから、運動と力の関係を求めるニュートン運動力学で表現できる。一つの着目するものだけを見つめてその変化を観察し、それから全体的なことを想像するやり方である。

これに対してオイラー的観察は、固定されたところで観察するのであるから、運動そのものを観察するわけではない。窓に出入りする量の時間的変化を観ることになる。これはあたかも季節の移ろいを部屋の中から窓を通じて観ていることと同じである。また、今月の家計簿の収入と支出の差がどうなっているのか？とみているようなものである。したがって、数学的には窓に対する出入りの差の時間変化だけで表すことになる。細かなことより総合的にどうなっているのかという見方である。

力というのはものの運動量を時間的に変化させるものである。運動量は質量×速度で表現される。ものの実体の運動のし易さ、し難さの程度を表すののとして質量がある。実体が時間的に変わらなければ運動量の時間変化は速度の時間変化で表され、すなわち加速度であるので、運動量の時間変化は質量×加速度と表わされる。この変化をもたらしたものが力である。単位は [ N ] であり、ニュートンと呼ぶ。

この力が作用している状態でものがその力の方向にある距離移動したとする。その時の力とその力の方向に移動した距離をかけたものが仕事である。したがって、仕事＝力×距離 [Nm] である。　なお、この単位 Nm をニュートン・メータと読む。この仕事をする能力をエネルギーという。エネルギーの単位は [ J ] である。これをジュールと読む。したがって、あるエネルギー E を持っていると、そのエネルギーでW の仕事ができるとみなされる。このことから、エネルギーの単位であるジュールと仕事の単位であるニュートン・メータは同じであることがわかる。たとえば、100 ジュールのエネルギーを持っていると、１ニュートンの力でものを100メートルの距離を動かせる能力を持っているとみなせる。また、10ニュートンの力を出せば10 メートル動かしてエネルギー切れとなる。

このエネルギーをどのくらいの時間(秒）で発生や消費をさせるかを表すのに、単位時間当たりのエネルギーで表したものを仕事率、もしくはパワー P と表現する。したがって、単位は [J/s] である。この [J/s ]を [W] （ワットと読む）で表す。Wは仕事の記号として使っている。そのため、単位のワットを表すには単位は鍵カッコ [ ]で囲って書くと間違いがない。ここで、[J ] = [Nm] で空き換えると [W]=[N・(m/s)]と書ける。すなわち、パワー＝力×速度 で表されることもある。

あるトルク T で軸の回転数が n [rpm] とするとき、この軸で出せるパワー（軸仕事率）P [W] は次のように表される。

ここで、ωは角速度である。

たとえば、車のエンジンスペックに回転数 n=6000 [rpm] でトルク T=200 [Nm]と書いてあったら、このエンジンで出せるパワー P [W] は上式から、 P = 2π×6000×200/60 = 126000 [W]　と求めることができる。これよりこのエンジンのパワーは、126 kW と表現するか、170 PS(馬力）と表現する。なお、1 PS =735.5 W の換算を用いた。

力のモーメントM は回転中心から R 離れた点に R 方向に直角に作用する力 F をかけて、　M=F×R で表される。いわゆる高校までに習うモーメントである。

これに対し、トルク T は工学でよく使われる言葉で、主に軸に加わるねじりに関して使われる。中心から r 離れた点に r 方向に直角に作用する力 f をかけて、T=f×r で表される。

上に示した図のようにトルクはモーメントで与えられるので、結局 T = M である。

コマの様に円盤が回転するとき、回転中心から r 離れた点の円周の接線方向速度（周速度）を v とする。回転の角速度を ω [rad/s]とするとき、それらの関係は次のように表せる。なお本来ベクトル量であるが、ここでは簡単に頭につける矢印を省いて表す。

なお、ω というのは1秒間に回った角度を表し、この時の角度を°(度）の代わりにrad（ラジアンと読む）で表す。したがって単位は [ rad/s ] である。１秒間に移動する距離のことを速度というのに対して、１秒間に回った角度のことを角速度という。度（°）とラジアンの換算は、一回転360度が2πに相当する。一般的に回転数を1分間にｎ 回転したとするとn [rpm] と表す。工学的には1秒間に換算して使うので、1分は60秒であるので、これをn/60 [rps]で表す。また、1回転というのは角度でいうと360度、すなわち2π ラジアンであるので、n 回転というのは2πn ラジアン回ったことになる。したがって、ωをnを使って書き換えると、

と表現できる。これを使って半径 r のところの周速度 v は次のように書ける。

したがって、 r 位置の周速度は回転数 n [rpm] と回転半径 r [m] に比例する。

ものが円運動を行うとき、遠心力がかかっているという表現をして、あたかも遠心力が円運動の根本であるような印象を受ける。小学校などで、水の入ったバケツを片手で持って、肩を中心にくるくると回すと水はバケツの底に張り付いていて、バケツがさかさまになっても水が落ちてこないことを体験する。水が張り付いているのは遠心力が作用しているからだと教えられるので、「回転運動＝遠心力」という構図が出来上がってしまっているからである。バケツを手で引っ張りながら回転させているのに、手の力のことを重視していない。想像するに、手で出している力はこの遠心力でものが飛んでいかないようにしているもので、二次的なものという意識があるのだと思う。ところが、よく考えてほしい。回しているのは手であって、ものを回転運動させているのは手なのである。したがって、手で出している力が主体であって、遠心力の方が副次的なものなのである。バケツに入った水がシステム（系）だとすると、それに外力として手で引っ張る力を作用させてまっすぐ進む方向を曲げているのである。速度ベクトルの方向を変えて加速度を発生させたのは手による外力なのである。

バケツは円の接線方向に真直ぐ移動しようとしているところを腕でその進行方向と直角な方向（円の中心方向）に引っ張ってその方向を変える。速度ベクトルの方向を変える力は速度の時間変化すなわち円の中心に向かう加速度を生じさせる。中心方向に引っ張る力(外力）はバケツの質量×加速度に相当する運動の変化を与える。この加速度は中心方向に向かっている。この中心方向に引っ張る力のことを「向心力」という。言い換えれば、向心力がバケツの質量×加速度の運動を生じさせる。加速による力が生じるとその力の方向とは真逆の方向に慣性力が作用する。たとえば、電車が発車するときに電車の加速方向とは逆の方向に体が引っ張られる経験があるであろう。この電車の加速と真逆方向にかかる力のことを慣性力という。先のバケツの例でいうと、向心力によって中心方向に加速を受け、言い換えれば中心に向かって加速するので、それとは逆方向すなわち中心から離れる方向に慣性力が作用する。これが「遠心力」である。遠心力は向心力が作用した結果として発生する二次的なものなのである。遠心力は向心力と同じ大きさであるが方向は逆である。力も大きさと方向という２つの情報を持つのでベクトルで表せる。ベクトルの角度が180°異なるので、片方を「＋」で表し、他を「ー」で表したとすると大きさが同じで符号が異なるのでバケツの水の重心で2つの力 F は打ち消しあって０となっている。つまり、合力の大きさが（＋F）＋（－F)=０となるので、方向を変える直前ではバケツは円の接線方向に真直ぐ移動しようとする。手を放して向心力を掛けなくすると遠心力も発生しないのでその時は、０＋０＝０であるので、真直ぐ接線方向に飛び出すことになる。ハンマー投げのハンマーが手を離した瞬間から円運動の接線方向に飛ぶのも同じ原理である

速さというのは単位時間あたりに進む距離のことである。したがって、単位は m/s である。つまり一秒間にどのくらいの距離を移動したかを表すのである。この時、どの方向に移動したかという方向という情報を含めたものを速度という言葉で表す。これを数学的には、ベクトル、つまり大きさと方向というもの（矢印の大きさと向き）で表す。正しくは速度を速度ベクトルといった方がよいが、聞きなれない言葉を付けるとかえって混乱するので、単に速度という。文字の頭に矢印を付けてベクトルを表す。太文字で書かれることもあるが、手書きでは書きづらいので頭に矢印を付ける。

大きさは

速度ベクトルの x 方向成分、および y 方向成分は

で表される。

角度(方向）は

である。

力には体積力と面積力がある。体積力は重力や電磁気力のようにものの内部の実体全体にわたって作用し、したがって体積に比例するような力である。これに対し、表面に垂直に作用する垂直力（圧力）や表面の接線方向に作用する摩擦力（せん断力）のように、ものの表面に作用する力が面積力である。

力はシステム(系）の外側（外界）から作用するので、外力という。これに対し、システムの内側(内界）に存在する分子間力や内界の分子が境界に衝突して発生する圧力やせん断応力などを内部の力、内力、という。外力によってものが変形する際に対抗して生じる内部応力をさす。応力は単位面積当たりの力として表す。

物の運動を調べるということは、速度の時間変化を観察することである。速度の時間変化は加速度である。速度が減少したら減速（符号としてはマイナス）、速度が増加したら増速（符号はプラス）という。では何が速度を変化させたのか？それがそのものの以外から作用した力なのである。ものの運動の大きさというものを表すのが運動量である。すなわち運動量は質量×速度で表される。実はこの運動量を変化させるものが力なのである。質量はものの動き易さとか動き難さを示す固有の性質である。決して重さを表すものではない。速度をv、質量をm、力を F で表すと、運動量はmvであり、その時間変化は時間 t の微分として表せるので、運動量の変化と力の関係は次のように表せる。

質量は時間的に変化しないとすると定数として微分の外に出せるので、結局、上式は次のように見慣れたものとなる。

つまり質量×加速度＝力のとなる。左辺は運動の時間変化であり、その変化を与えたのが右辺の力ということになる。これが質量 m の物体の運動方程式である。

したがって、ものの速度の時間変化を調べることはそれにどのような力が作用したのかを知ることになるのである。これが観察の目的である。